If the sides a, b, c of a ∆ABC is in H.P., prove that are in H.P.

As a, b, c is in HP (given)

So, are in AP

Hence

Let a, b, c be the sides of any triangle ABC. Then by applying the sine rule, we get

So, a = k sin A, b = k sin B, c = k sin C…(ii)

Substituting equation (ii) in equation (i), we get

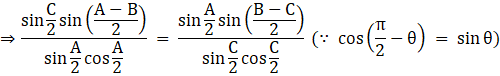
By cross multiplying we get

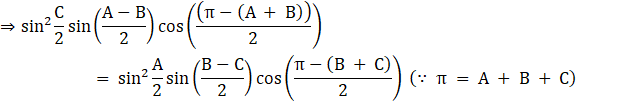
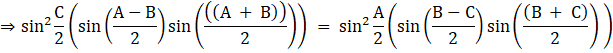
Now, so above equation becomes,

so the above equation becomes

Divide both sides by , we get

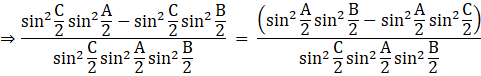
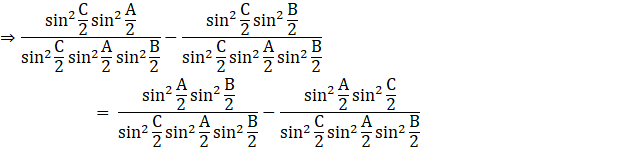
Now canceling the like terms we get

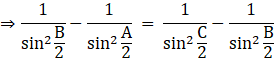
Hence are in AP

Therefore,

are in HP

Hence proved