Prove the following by the principle of mathematical induction:

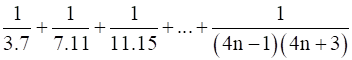
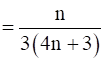
Let P(n):

For n= 1is true

P(1): =

Since, P(n) is true for n =1

Let P(n) is true for n= k

P(n): - - - - - - - (1)

We have to show that,

Now,

=

=

=

=

=

=

=

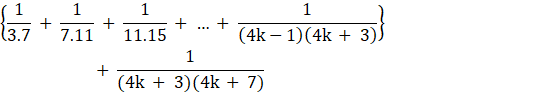
Therefore, P(n) is true for n = k + 1

Hence, P(n) is true for all n∈ N