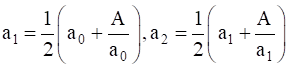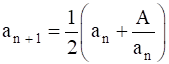Given and for n ≥ 2, where a > 0, A > 0.

Prove that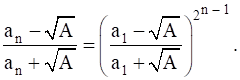

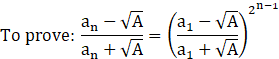
Step1: For n=1

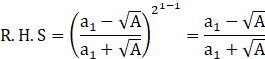
As LHS=RHS.

So, it is true for P(1)

For n=k, let P(k) be true.

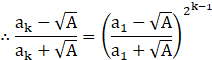
Now, we need to show P(k+1) is true whenever P(k) is true.

P(k+1):

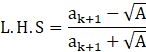
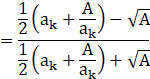
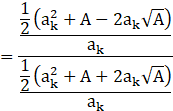
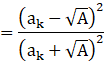
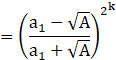
As L.H.S=R.H.S

Thus, P(k+1) is true. So, by the principle of mathematical induction

P(n) is true for all n.