Show that the points (5, 5), (6, 4), (- 2, 4) and (7, 1) all lie on a circle, and find its equation, centre, and radius.

Given that we need to show the points A(5,5), B(6,4), C(- 2,4) and D(7,1) lie on a circle.

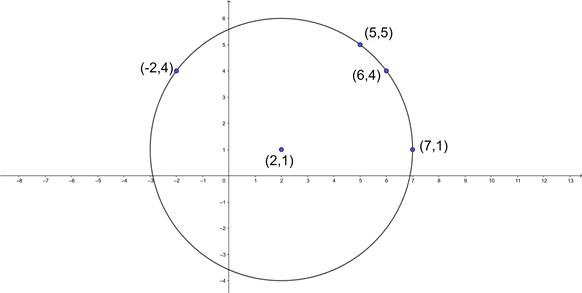
Let us make a circle with any three points and check whether the fourth point lies on it or not.

Let us assume the circle passes through the points A, B, C.

We know that the standard form of the equation of the circle is given by:

⇒ x² + y² + 2ax + 2by + c = 0 ..... (1)

Substituting A(5,5) in (1), we get,

⇒ 5² + 5² + 2a(5) + 2b(5) + c = 0

⇒ 25 + 25 + 10a + 10b + c = 0

⇒ 10a + 10b + c + 50 = 0 ..... (2)

Substituting B(6,4) in (1), we get,

⇒ 6² + 4² + 2a(6) + 2b(4) + c = 0

⇒ 36 + 16 + 12a + 8b + c = 0

⇒ 12a + 8b + c + 52 = 0 .....(3)

Substituting C(- 2,4) in (1), we get,

⇒ (- 2)² + 4² + 2a(- 2) + 2b(4) + c = 0

⇒ 4 + 16 - 4a + 8b + c = 0

⇒ 20 - 4a + 8b + c = 0

⇒ 4a - 8b - c - 20 = 0 .....(4)

On solving (2), (3) and (4) we get,

⇒ a = - 2, b = - 1 and c = - 20

Substituting these values in (1), we get

⇒ x² + y² + 2(- 2)x + 2(- 1)y - 20 = 0

⇒ x² + y² - 4x - 2y - 20 = 0 ..... (5)

Substituting D(7,1) in eq(5) we get,

⇒ 7² + 1² - 4(7) - 2(1) - 20

⇒ 49 + 1 - 28 - 2 - 20

⇒ 0

∴ The points (3, - 2), (1,0), (- 1, - 2), (1, - 4) lie on a circle.

We know that for a circle x² + y² + 2ax + 2by + c = 0,

⇒ Centre = (- a, - b)

⇒ Radius =

Comparing (5) with (1), we get

⇒ Centre =

⇒ Centre = (2,1)

⇒ Radius =

⇒ Radius =

⇒ Radius = 5.

∴ The centre and radius of the circle is (2, 1) and 5.