Find the equation of the circle which circumscribes the triangle formed by the lines:

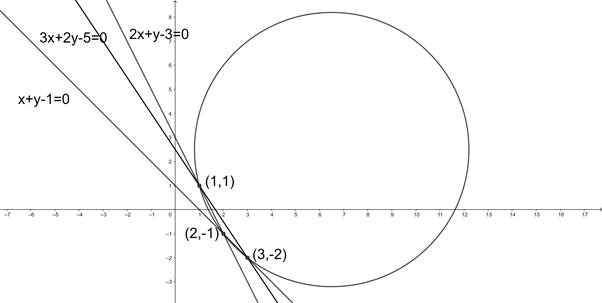
2x + y - 3 = 0, x + y - 1 = 0 and 3x + 2y - 5 = 0

Given that we need to find the equation of the circle formed by the lines:

⇒ 2x + y - 3 = 0

⇒ x + y - 1 = 0

⇒ 3x + 2y - 5 = 0

On solving these lines we get the intersection points A(2, - 1), B(3, - 2), C(1,1)

We know that the standard form of the equation of a circle is given by:

⇒ x² + y² + 2ax + 2by + c = 0 .....(1)

Substituting (2, - 1) in (1), we get

⇒ 2² + (- 1)² + 2a(2) + 2b(- 1) + c = 0

⇒ 4 + 1 + 4a - 2b + c = 0

⇒ 4a - 2b + c + 5 = 0 ..... (2)

Substituting (3, - 2) in (1), we get

⇒ 3² + (- 2)² + 2a(3) + 2b(- 2) + c = 0

⇒ 9 + 4 + 6a - 4b + c = 0

⇒ 6a - 4b + c + 13 = 0 ..... (3)

Substituting (1,1) in (1), we get

⇒ 1² + 1² + 2a(1) + 2b(1) + c = 0

⇒ 1 + 1 + 2a + 2b + c = 0

⇒ 2a + 2b + c + 2 = 0 ..... (4)

Solving (2), (3), (4) we get

⇒ .

Substituting these values in (1), we get

⇒

⇒ x² + y² - 13x - 5y + 16 = 0

∴ The equation of the circle is x² + y² - 13x - 5y + 16 = 0.