If an A.P. is such that 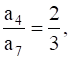find .

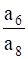Given:

To find:

We know, a_n = a + (n – 1)d where a is a first term or a₁ and d is the common difference and n is any natural number

When n = 4:

∴ a₄ = a + (4 – 1)d

⇒ a₄ = a + 3d

When n = 6:

∴ a₆ = a + (6 – 1)d

⇒ a₆ = a + 5d

When n = 7:

∴ a₇ = a + (7 – 1)d

⇒ a₇ = a + 6d

When n = 8:

∴ a₈ = a + (8 – 1)d

⇒ a₈ = a + 7d

According to the question:

⇒ 3(a + 3d) = 2(a + 6d)

⇒ 3a + 9d = 2a + 12d

⇒ 3a – 2a = 12d – 9d

⇒ a = 3d

Now,

Hence, the value of