find the equation of the ellipse in the following cases:

eccentricity and length of latus - rectum = 5

Given that we need to find the equation of the ellipse whose eccentricity is and length of latus rectum is 5.

Let us assume the equation of the ellipse as (a²>b²).

We know that eccentricity(e) =

⇒

⇒

⇒

⇒

We know that the length of the latus rectum is .

⇒

⇒

⇒

⇒

⇒

⇒

⇒

⇒

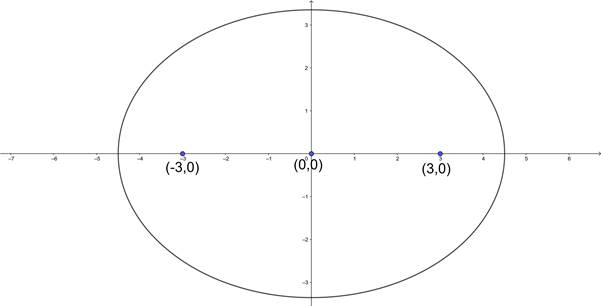
The equation of the ellipse is

⇒

⇒

⇒

⇒ 20x² + 36y² = 405

∴ The equation of the ellipse is 20x² + 36y² = 405.