Find the equation of the ellipse whose centre is (- 2, 3) and whose semi - axis are 3 and 2 when the major axis is (i) parallel to x - axis (ii) parallel to the y - axis.

Given that we need to find the equation of the ellipse whose centre is (- 2,3) and whose semi - axis are 3 and 2.

(i) If major axis is parallel to the x - axis.

We know that the equation of the ellipse with centre (p,q) is given by .

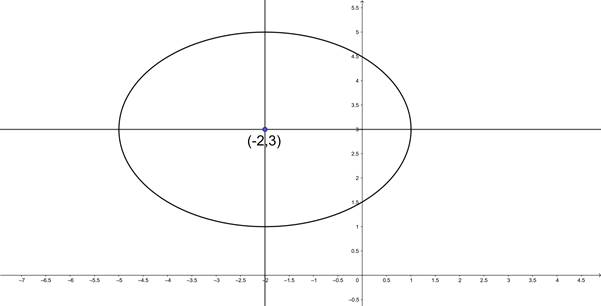
Since major axis is parallel to x - axis a²>b².

So, a = 3 and b = 2.

⇒ a² = 9

⇒ b² = 4

The equation of the ellipse is

⇒

⇒

⇒ 4(x² + 4x + 4) + 9(y² - 6y + 9) = 36

⇒ 4x² + 16x + 16 + 9y² - 54y + 81 = 36

⇒ 4x² + 9y² + 16x - 54y + 61 = 0

∴ The equation of the ellipse is 4x² + 9y² + 16x - 54y + 61 = 0.

(ii) If major axis is parallel to the y - axis.

We know that the equation of the ellipse with centre (p,q) is given by .

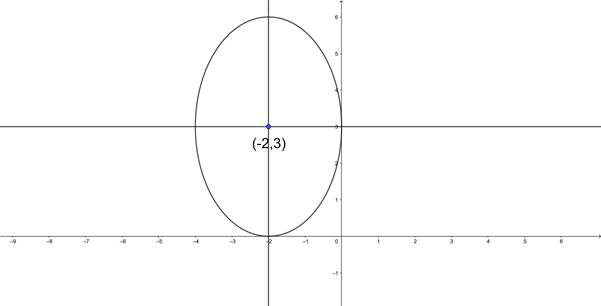
Since major axis is parallel to y - axis b²>a².

So, a = 2 and b = 3.

⇒ a² = 4

⇒ b² = 9

The equation of the ellipse is

⇒

⇒

⇒ 9(x² + 4x + 4) + 4(y² - 6y + 9) = 36

⇒ 9x² + 36x + 36 + 4y² - 24y + 36 = 36

⇒ 9x² + 4y² + 36x - 24y + 36 = 0

∴ The equation of the ellipse is 9x² + 4y² + 36x - 24y + 36 = 0.