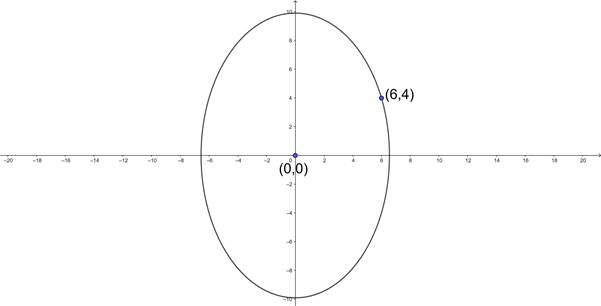
Find the equation of an ellipse with its foci on y - axis, eccentricity 3/4, centre at the origin and passing through (6, 4).

Given that we need to find the equation of the ellipse whose eccentricity is , centre at the origin and passes through (6,4).

Let us assume the equation of the ellipse is - - - - (1) (a²<b²), since centre is at origin and foci on y - axis.

We know that eccentricity of the ellipse is

⇒

⇒

⇒ 16b² - 16a² = 9b²

⇒ 7b² = 16a²

⇒ ..... - - - (2)

Substituting the point (6,4) in (1) we get,

⇒

⇒

⇒

⇒

⇒ 7b² = 688

⇒

From (2),

⇒

⇒

⇒ a² = 43

The equation of the ellipse is

⇒

⇒

⇒

⇒ 16x² + 7y² = 688

∴ The equation of the ellipse is 16x² + 7y² = 688.