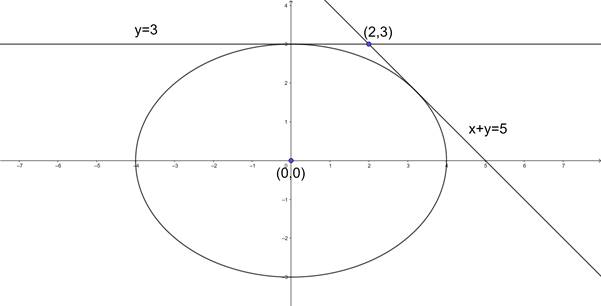
The equations of the tangents to the ellipse 9x² + 16y² = 144 from the point (2, 3) are

Given that we need to find the equation of the tangents to the ellipse 9x² + 16y² = 144 from the point (2,3).

We know that tangent at any point (x₁,y₁) on the ellipse is S₁ = 0.

⇒ S₁ = 0

⇒ 9(xx₁) + 16(yy₁) = 144 .... (1)

This passes through the point (2,3)

⇒ 9(2x₁) + 16(3y₁) = 144

⇒ 18x₁ + 48y₁ = 144

⇒ 3x₁ + 8y₁ = 24

⇒ 8y₁ = 24 - 3x₁

⇒ .... - - (2)

Substituting this in the equation of the ellipse we get,

⇒

⇒

⇒

⇒

⇒

⇒

⇒

From (2)

⇒

⇒ y₁ = 3

⇒

⇒

⇒

Substituting x₁ = 0 and y₁ = 3 in (1), we get

⇒ 9(x(0)) + 16(y(3)) = 144

⇒ 48y = 144

⇒ y = 3.

Substituting and in (1), we get

⇒

⇒

⇒ x + y = 5

∴ The correct option is D