A large window has the shape of a rectangle surmounted by an equilateral triangle. If the perimeter of the window is 12 metres find the dimensions of the rectangle that will produce the largest area of the window.

Question

Philoid · Accepted Answer

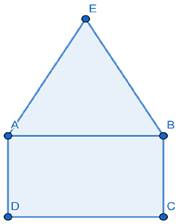
Let the side of equilateral triangle, length and breadth of rectangle be a, x and y respectively

AE = AB = a (ABE is equilateral triangle)

AB = x = a (triangle is mounted over rectangle) …1

AD = y

Perimeter of window = 12 m (given)

AE + EB + BC + CD + DA = 12

a + a + y + x + y = 10

2a + 2y + x = 10

3x + 2y = 12 (from equation 1)

… 2

To admit maximum amount of light, area of window should be maximum

Assuming area of window as A

A = xy +

(from equation 1 & 2)

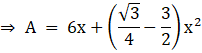
Condition for maxima and minima is

= 0

x =

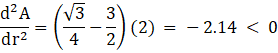
For x = A will be maximum.

Length of rectangular part = (from equation 1)

Breath of rectangular part = (from equation 2)
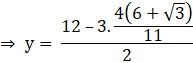