Show that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is .

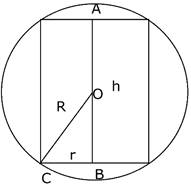
Let the radius, height and volume of cylinder be r, h and V respectively

Radius of sphere = R (Given)

Volume of cylinder, V = πr²h …1

OC = R

BC = r

In triangle OBC,

+ r² = R²

r² = R² - …2

Replacing equation 2 in equation 1, we get

V = π (R² - )(h) = πR²h -

Condition for maxima and minima is

= 0

Since, h cannot be negative

Hence,

For < 0

V will be maximum for