Show that the cone of the greatest volume which can be inscribed in a given sphere has an altitude equal to 2/3 of the diameter of the sphere.


Let the radius and height of cone be r and h respectively


Radius of sphere = R



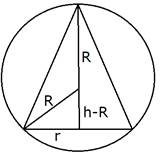
R2 = r2 + (h - R)2


R2 = r2 + h2 + R2 - 2hR


r2 = 2hR - h2 …1


Assuming volume of cone be V


Volume of cone, (from equation 1)



Condition for maxima and minima is




⇒ 4hR - 3 h2= 0



For , < 0


V will be maximum for



20
1