Prove that the least perimeter of an isosceles triangle in which a circle of radius r can be inscribed is 6√3r.

Question

Philoid · Accepted Answer

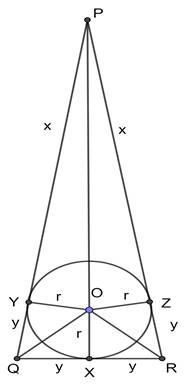
Let PQR is the triangle with inscribed circle of radius ‘r’, touching sides PQ at Y, QR at X and PR at Z.

OZ, OX, OY are perpendicular to the sides PR,QR,PQ.

Here PQR is an isosceles triangle with sides PQ = PR and also from the figure,

⇒ PY = PZ = x

⇒ YQ = QX = XR = RZ = y

From the figure we can see that,

⇒ Area(ΔPQR) = Area(ΔPOR) + Area(ΔPOQ) + Area(ΔQOR)

We know that area of a triangle = ×base×height

⇒

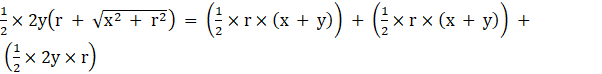
⇒ …… (1)

We know that perimeter of the triangle is Per = PQ + QR + RP

⇒ PER = (x + y) + (x + y) + 2y

⇒ PER = 2x + 4y …… (2)

From(1)

⇒

We need perimeter to be minimum and let us PER as the function of y,

We know that for maxima and minima ,

⇒

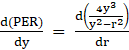
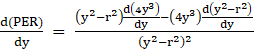
⇒ 4y⁴ - 12y²r² = 0

⇒ 4y²(y² - 3r²) = 0

⇒

Differentiating PER again,

⇒

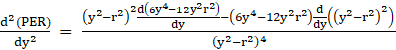
⇒ >0(minima)

We got minima at y = r.

Let’s find the value of x,

⇒

⇒ x = r

⇒ PER = 2(r) + 4(r)

⇒ PER = 6r

∴ Thus proved