Evaluate the following :

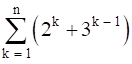
The given expression can also be written as

⇒ …(1)

⇒

Now this term is in GP.

2, 4, 8…to n terms

∴ Common Ratio =

∴ Sum of GP for n terms = …(2)

⇒ a = 2, r = 2, n = n

∴ Substituting the above values in (2) we get,

⇒

⇒ 2^{n + 1} – 2.

⇒

Now this term is in GP.

1, 3, 9…to n terms

∴ Common Ratio = r =

∴ Sum of GP for n terms = …(2)

⇒ a = 1, r = 3, n = n

∴ Substituting the above values in (2) we get,

⇒

⇒

Now, Adding both these we will get the required solution.

⇒ 2^{n + 1} – 2 +

⇒