Find the sum of the series whose nth term is :

n³ – 3ⁿ

Generalized term be n³ – 3ⁿ

1^st term = (1)³ – 3⁽¹⁾

2^nd term = (2)³ – 3⁽²⁾

And so on

nth term= n³ – 3ⁿ

general term= r³ – 3^r

Summation=1^st term + 2^nd term + …… + nth term

=(1)³ – 3⁽¹⁾ + (2)³ – 3⁽²⁾ + ……… + n³ – 3ⁿ………(1)

We know

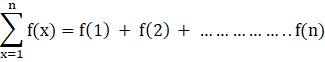
Thus

From (1) we have

Summation =

We know by property that:

∑axⁿ + bx^{n - 1} + cx^{n - 2}…….d₀=a∑xⁿ + b∑x^{n - 1} + c∑x^{n - 2}…….. + d₀∑1

Thus

………(2)

We know,

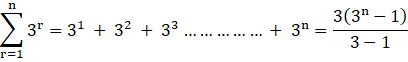
Since, where if

Thus substituting the above values in (2)

Summation