Evaluate the following integrals as a limit of sums:

![]()
Formula used:
![]()
where,
![]()
Here, a = 1 and b = 4
Therefore,
![]()
![]()
Let,
![]()
Here, f(x) = 3x2 + 2x and a = 1
![]()
Now, by putting x = 1 in f(x) we get,
f(1) = 3(1)2 + 2(1) = 3 + 2 = 5
f(1 + h)
= 3(1 + h)2 + 2(1 + h)
= 3{h2 + 12 + 2(h)(1)} + 2 + 2h
= 3h2 + 3 + 6h + 2 + 2h
= 3h2 + 8h + 5
Similarly, f(1 + 2h)
= 3(1 + 2h)2 + 2(1 + 2h)
= 3{(2h)2 + 12 + 2(2h)(1)} + 2 + 4h
= 3(2h)2 + 3 + 6(2h) + 2 + 2(2h)
= 3(2h)2 + 8(2h) + 5
{∵ (x + y)2 = x2 + y2 + 2xy}
![]()
![]()
Since 5 is repeating n times in series
![]()
Now take 3h2 and 8h common in remaining series
![]()
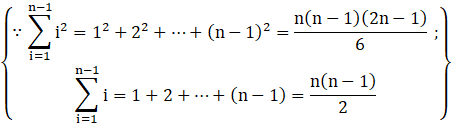
![]()
Put,
![]()
Since,
![]()
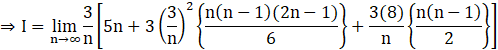
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
20