A medical company has factories at two places, A and B. From these places, supply is made to each of its three agencies situated at P, Q and R. The monthly requirements of the agencies are respectively, 40, 40 and 50 packets of the medicines, while the production capacity of the factories, A and B are 60 and 70 packet respectively. The transportation cost per packet from the factories to the agencies are given below :

How many packets from each factory be transported to each agency so that the cost of transportation is minimum? Also find the minimum cost?

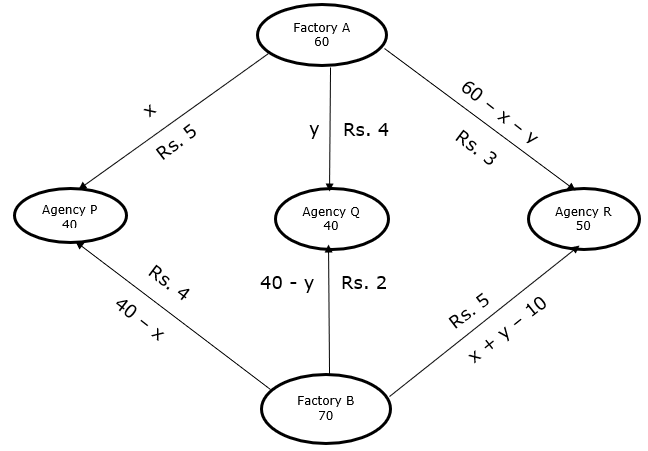
Let factory A supply x and y packets of medicines to agency P and Q respectively. Remaining packets of factory A are 60 – x – y. So, now they will be supplied to agency R by factory A.

Now, remaining packets requirement of agency P is 40 – x which will be supplied by factory B.

Remaining packets requirement of agency Q is 40 – y which will be supplied by factory B.

Remaining packets requirement of agency R is 50 – (60 – x – y)

= x + y – 10 which will be supplied by factory B.

where,

x ≥ 0, y ≥ 0 and 60 – x – y ≥ 0

⇒ x ≥ 0, y ≥ 0 and x + y ≤ 60

40 – x ≥ 0, 40 – y ≥ 0 and x + y – 10 ≥ 0

⇒x ≤ 40, y ≤ 40 and x + y ≥ 10

This can be illustrated by this:

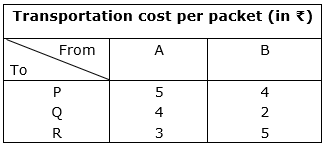
Cost = Number of packets * Cost of transportation per packet

Total transportation cost z is given by,

z = 5x + 4y + 3(60 – x – y) + 4(40 – x) + 2(40 – y) + 5(x + y – 10)

⇒ z = 5x + 4y + 180 – 3x – 3y + 160 – 4x + 80 – 2y + 5x + 5y – 50

⇒ z = 3x + 4y + 370

We need to minimize the cost

Hence, mathematical formulation of LPP is

Minimize z = 3x + 4y + 370

subject to the constraints,

x+y≥10

y≤40

x≤40

x+y≤60

x,y≥0

The feasible region determined by the system of constraints is as follows:

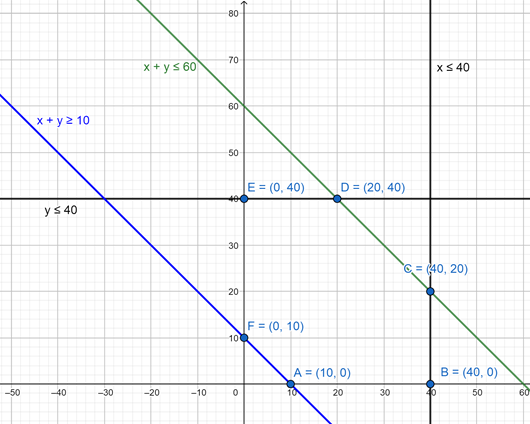
The corner points of the enclosed region are A(10, 0) , B(40, 0), C(40, 20), D(20,40), E(0, 40) and F(0, 10)

The value of z at these corners points is as follows:

Case 1: A(10, 0)

z = 3x + 4y + 370

⇒ z = 3(10) + 4(0) + 370

⇒ z = 30 + 0 + 370

⇒ z = 400

Case 2: B(40, 0)

z = 3x + 4y + 370

⇒ z = 3(40) + 4(0) + 370

⇒ z = 120 + 0 + 370

⇒ z = 490

Case 3: C(40, 20)

z = 3x + 4y + 370

⇒ z = 3(40) + 4(20) + 370

⇒ z = 120 + 80 + 370

⇒ z = 570

Case 4: D(20, 40)

z = 3x + 4y + 370

⇒ z = 3(20) + 4(40) + 370

⇒ z = 60 + 160 + 370

⇒ z = 590

Case 5: E(0, 40)

z = 3x + 4y + 370

⇒ z = 3(0) + 4(40) + 370

⇒ z = 0 + 160 + 370

⇒ z = 530

Case 4: F(0, 10)

z = 3x + 4y + 370

⇒ z = 3(0) + 4(10) + 370

⇒ z = 0 + 40 + 370

⇒ z = 410

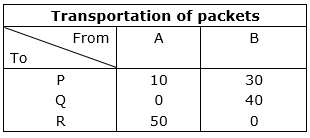
The value of z is minimum in first case at point A(10, 0)

As, x = 10, y = 0

Factory A supplies to:

Agency P = x = 10 packets

Agency Q = y = 0 packets

Agency R = 60 – x – y = 60 – 10 – 0 = 50 packets

Godown B supplies to:

Agency P = 40 – x = 40 – 10 = 30 packets

Agency Q = 40 – y = 40 – 0 = 40 packets

Agency R = x + y – 10 = 10 + 0 – 10 = 0 packets

Minimum cost for transportation of these packets to their respective agencies = Rs. 400