The base of an equilateral triangle with side 2a lies along the y-axis such that the mid-point of the base is at the origin. Find

the vertices of the triangle.

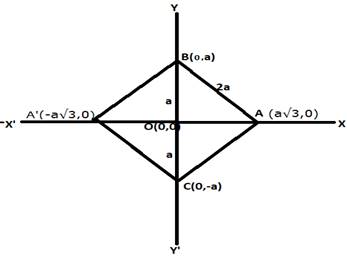
Given that the base of the equilateral triangle is on the y-axis and mid-point of the base is at the origin, so its figure will be like this as shown.

So here, O(0,0) is the midpoint of the base.

An equilateral triangle has all sides equal so if O is the mid-point of the base BC, so B and C are the two vertices of the triangle. Now we have two vertices of the triangle, which is the base of equilateral triangle lying on the y-axis. Now if base in on y-axis then x-axis are as bisector of the base and so our third vertices will be on the x-axis either left or right.

So now in right ∆BOA

Pythagoras Theorem: In a right-angled triangle the square of the biggest side(hypotenuse) equals the sum of the squares of the other two sides(Perpendicular and base).

BO² + OA² = AB² { By Pythagoras theorem}

a² + OA² = (2a) ²

OA² = 4a²- a²

OA² = 3a²

OA = ±a√3

So vertices of triangle are A(±a√3,0) B(0,a)and C(0,-a).