Prove that the point (4,8), (0,2), (3,0) and (7,6) are the vertices of a rectangle.
Note that to show that a quadrilateral is a rectangle, it is sufficient to show that
(a) ABCD is a parallelogram, i.e., AC and BD bisect each other and,
(b) the diagonal AC and BD are equal
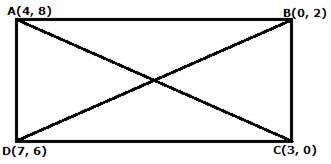
Let A(4, 8), B(0, 2), C(3, 0) and D(7, 6) are the vertices of a rectangle.
Coordinates of the midpoint of AC are
![]()
Coordinates of the midpoint of BD are
![]()
Thus, AC and BD have the same midpoint.
Hence, ABCD is a parallelogram
Now, check for the diagonals by using the distance formula
AC = √(3 – 4)2 + (0 – 8)2
= √(-1)2 + (-8)2
= √1 + 64
= √65 units
and
BD = √(7 - 0)2 + (6 – 2)2
⇒ BD = √(7)2 + (4)2
⇒ BD = √49 + 16
⇒ BD = √65 units
∴ AC = BD
Hence, ABCD is a rectangle.
27