The slope of a line is double of the slope of another line. If tangents of the angle between them is 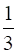, find the slopes of the other line.

Given, The tangent of the angle between them is

To Find Slope of the other line.

Assumption: The slope of line m₁ = x, and m₂ = 2x

Formula used:

Explanation: We have tan given, then

Case 1:

2x² + 1 = 3x – 6x

2x² + 3x + 1 = 0

2x² + 2x + x + 1 = 0

2x(x + 1) + 1(x + 1) = 0

(2x + 1)(x + 1) = 0

x = – 1,

Case 2:

2x² + 1 = 3x

2x² – 3x + 1 = 0

2x^{2 –} 2x – x + 1 = 0

2x(x – 1) – 1(x – 1) = 0

(2x – 1)(x – 1) = 0

x = 1,

Hence, The slope of other line is either 1, or – 1, .