A quadrilateral has vertices (4, 1), (1, 7), (– 6, 0) and (– 1, – 9). Show that the mid – points of the sides of this quadrilateral form a parallelogram.

Question

Philoid · Accepted Answer

Given, A quadrilateral has vertices (4, 1), (1, 7), (– 6, 0) and (– 1, – 9).

To Prove: Mid – Points of the quadrilateral form a parallelogram.

The formula used: Mid point formula =

Explanation: Let ABCD is a quadrilateral

E is the midpoint of AB

F is the midpoint of BC

G is the midpoint of CD

H is the midpoint of AD

Now, Find the Coordinates of E, F,G and H using midpoint Formula

Coordinate of E =

Coordinate of F =

Coordinate of G =

Coordinate of H =

Now, EFGH is a parallelogram if the diagonals EG and FH have the same mid – point

Coordinate of mid – point of EG =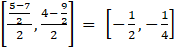

Coordinate of mid – point of FH =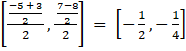

Since Diagonals are equals then EFGH is a parallelogram.

Hence, EFGH is a parallelogram.