Find the sum of the following series to infinity :

We observe that above progression possess a common ratio, but alternatively , adjacent terms are not possessing a common ratio. So, it consists of 2 geometric progressions.

Let, S =

⇒ S =

Let us denote the two progressions with S₁ and S₂

∴ S = S₁ + S₂

S₁ =

Common ratio = r =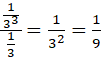

Sum of infinite GP = ,where a is the first term and r is the common ratio.

Note: We can only use the above formula if |r|<1

Clearly, a = and r = 1/9

⇒ S₁ =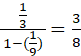

S₂ =

Common ratio = r =

Sum of infinite GP = ,where a is the first term and r is the common ratio.

Note: We can only use the above formula if |r|<1

Clearly, a = and r = 1/25

⇒ S₂ =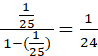

Hence,

S =