If a, b, c are in G.P., then prove that :

Question

Philoid · Accepted Answer

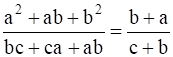
As a,b,c are in GP

Note:

1. In general, the GP series is like a,ar,ar²……….

2. In this, b = ar and c = br = ar²

So we proceed forward with the aim to equalize LHS and RHS of the equation to be proved using the above ideas.

L.H.S =

⇒ LHS =

Now

R.H.S =

⇒ RHS =

∴ RHS = 1/r

Clearly we observed that,

LHS = RHS = (1/r) …Proved