Find the derivative of f(x) = cos x at x = 0

Derivative of a function f(x) at any real number a is given by –

{where h is a very small positive number}

∴ derivative of cos x at x = 0 is given as –

∵ we can’t find the limit by direct substitution as it gives 0/0 (indeterminate form)

So we need to do few simplifications to evaluate the limit.

As we know that 1 – cos x = 2 sin²(x/2)

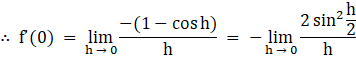
Dividing the numerator and denominator by 2 to get the form (sin x)/x to apply sandwich theorem, also multiplying h in numerator and denominator to get the required form.

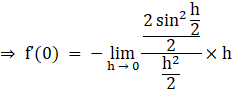
Using algebra of limits we have –

Use the formula:

∴ f’(0) = – 1×0 = 0

Hence,

Derivative of f(x) = cos x at x = 0 is 0