Differentiate each of the following from first principles:

Question

Philoid · Accepted Answer

We need to find derivative of f(x) = √(2x² + 1)

Derivative of a function f(x) from first principle is given by –

f’(x) = {where h is a very small positive number}

∴ derivative of f(x) = √(2x² + 1) is given as –

f’(x) =

⇒ f’(x) =

As the above limit can’t be evaluated by putting the value of h because it takes 0/0 (indeterminate form)

∴ multiplying denominator and numerator by to eliminate the indeterminate form.

⇒ f’(x) =

Using algebra of limits & a² – b² = (a + b)(a – b),we have –

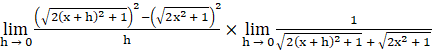
⇒ f’(x) =

Using a² – b² = (a + b)(a – b), we have –

⇒ f’(x) =

Evaluating the limit by putting h = 0

∴ f’(x) =

Hence,

Derivative of f(x) = √(2x² + 1)