Differentiate the following from first principles

Question

Philoid · Accepted Answer

We need to find derivative of f(x) =

Derivative of a function f(x) from first principle is given by –

f’(x) = {where h is a very small positive number}

∴ derivative of f(x) = is given as –

f’(x) =

⇒ f’(x) =

Use: sin A – sin B = 2 cos ((A + B)/2) sin ((A – B)/2)

⇒ f’(x) =

Using algebra of limits, we have –

⇒ f’(x) = 2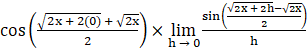

⇒ f’(x) =

As, h → 0 ⇒ → 0

∴ To use the sandwich theorem to evaluate the limit, we need in denominator. So multiplying this in numerator and denominator.

⇒ f’(x) =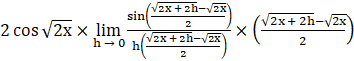

Using algebra of limits –

⇒ f’(x) =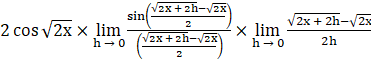

Use the formula:

∴ f’(x) = × 1 ×

⇒ f’(x) =

Again we get an indeterminate form, so multiplying and dividing √(2x + 2h) + √(2x) to get rid of indeterminate form.

∴ f’(x) =

Using a² – b² = (a + b)(a – b), we have –

⇒ f’(x) =

Using algebra of limits we have –

⇒ f’(x) =

∴ f’(x) =

Hence,

Derivative of f(x) = sin √2x =