Differentiate each of the following functions by the product by the product rule and the other method and verify that answer from both the methods is the same.

(3 sec x – 4 cosec x) ( – 2 sin x + 5 cos x)

Let, y = (3 sec x – 4 cosec x)( – 2 sin x + 5 cos x)

⇒ y = – 6 sec x sin x + 15 sec x cos x + 8 sin x cosec x – 20cosec x cos x

⇒ y = – 6tan x + 15 + 8 – 20 cot x {∵ tan x cos x = sin x}

⇒ y = – 6 tan x – 20 cot x + 23

Differentiating y w.r.t x –

Using algebra of derivatives, we have –

Use formula of derivative of above function to get the result.

⇒

∴ …equation 1

Derivative using product rule –

We have to find dy/dx

As we can observe that y is a product of two functions say u and v where,

u = (3 sec x – 4 cosec x) and v = ( – 2 sin x + 5 cos x)

∴ y = uv

As we know that to find the derivative of product of two function we apply product rule of differentiation.

By product rule, we have –

…equation 2

As, u = (3 sec x – 4 cosec x)

∴

Use the formula: &

⇒

⇒ …..equation 3

As, v = – 2 sin x + 5 cos x

⇒

⇒ …equation 4 {∵ }

∴ from equation 2, we can find dy/dx

∴

using equation 3 & 4, we get –

⇒

∵ sin x = tan x cos x , so we get –

⇒

⇒

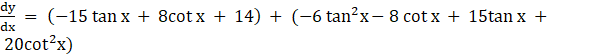
⇒ = 20(1 + cot² x) – 6(1 + tan² x)

∴ [∵ 1 + tan² x = sec² x & 1 + cot² x = cosec² x ]

∴

Hence,

….equation 5

Clearly from equation 1 and 5 we observed that both equations gave identical results.

Hence, Results are verified