Differentiate the following functions with respect to x:

Question

Philoid · Accepted Answer

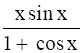
Let, y =

We have to find dy/dx

As we can observe that y is a fraction of two functions say u and v where,

u = x sin x and v = 1 + cos x

∴ y = u/v

As we know that to find the derivative of fraction of two function we apply quotient rule of differentiation.

By quotient rule, we have –

…equation 1

As, u = x sin x

∵ u is the product of two function x and tan x, so we will be applying product rule of differentiation –

∴

⇒ [using product rule]

∵ , So we get –

⇒ …equation 2

As, v = 1 + cos x

∵ , so we get –

…equation 3

∴ from equation 1, we can find dy/dx

∴

using equation 2 and 3, we get –

⇒

Hence,