Prove that the straight lines (a + b)x + (a – b)y = 2ab, (a – b)x + (a + b)y = 2ab and x + y = 0 form an isosceles triangle whose vertical angle is .

Given:

The given lines are

(a + b) x + (a − b) y = 2ab … (1)

(a − b) x + (a + b) y = 2ab … (2)

x + y = 0 … (3)

To prove:

The straight lines (a + b)x + (a – b)y = 2ab, (a – b)x + (a + b)y = 2ab and x + y = 0 form an isosceles triangle whose vertical angle is

Assuming:

Let m₁, m₂ and m₃ be the slopes of the lines (1), (2) and (3), respectively.

Explanation:

Now,

Slope of the first line = m₁

Slope of the second line = m₂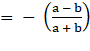

Slope of the third line = m₃ = -1

Let θ₁ be the angle between lines (1) and (2), θ₂ be the angle between lines (2) and (3) and θ₃ be the angle between lines (1) and (3).

∴

⇒

⇒

∴

⇒

⇒

∴

⇒

⇒

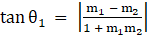
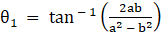
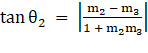
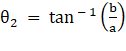
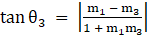
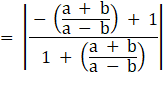
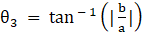
Here,
θ₂ = θ₃ and

Hence proved, the given lines form an isosceles triangle whose vertical angle is