Find the values of α so that the point P(α 2, α) lies inside or on the triangle formed by the lines x – 5y + 6 = 0, x – 3y + 2 = 0 and x – 2y – 3 = 0.
Given: x – 5y + 6 = 0, x – 3y + 2 = 0 and x – 2y – 3 = 0 forming a triangle and point P(α2, α) lies inside or on the triangle
To find: value of α
Explanation:
Let ABC be the triangle of sides AB, BC and CA whose equations are x − 5y + 6 = 0, x − 3y + 2 = 0 and x − 2y − 3 = 0, respectively.
On solving the equations,
We get A (9, 3), B (4, 2) and C (13, 5) as the coordinates of the vertices.
Diagram:
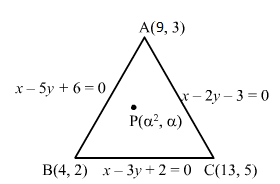
It is given that point P (α2, α) lies either inside or on the triangle. The three conditions are given below.
(i) A and P must lie on the same side of BC.
(ii) B and P must lie on the same side of AC.
(iii) C and P must lie on the same side of AB.
If A and P lie on the same side of BC, then
(9 – 9 + 2)(α2 – 3α + 2) ≥0
⇒ (α – 2)(α – 1) ≥ 0
⇒ α ∈ (- ∞, 1 ] ∪ [ 2, ∞) … (1)
If B and P lie on the same side of AC, then
(4 – 4 – 3) (α2 – 2α – 3) ≥ 0
⇒ (α – 3)(α + 1) ≤ 0
⇒ α ∈ [- 1, 3] … (2)
If C and P lie on the same side of AB, then
(13 – 25 + 6)(α2 – 5α + 6) ≥0
⇒ (α – 3)(α – 2) ≤ 0
⇒ α ∈ [ 2, 3] … (3)
From (1), (2) and (3), we get:
α∈ [ 2, 3]
Hence, α∈ [2, 3]