Find the equation of the straight line which passes through the point of intersection of the lines 3x – y = 5 and x + 3y = 1 and makes equal and positive intercepts on the axes.

Question

Philoid · Accepted Answer

Given:

Lines 3x – y = 5 and x + 3y = 1

To find:

The equation of the straight line which passes through the point of intersection of the lines 3x – y = 5 and x + 3y = 1 and makes equal and positive intercepts on the axes.

Explanation:

The equation of the straight line passing through the point of intersection of 3x − y = 5 and x + 3y = 1 is

3x − y − 5 + λ(x + 3y − 1) = 0

⇒ (3 + λ)x + (− 1 + 3λ)y − 5 − λ = 0 … (1)
⇒ y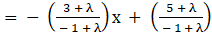

The slope of the line that makes equal and positive intercepts on the axis is − 1.

From equation (1), we have:

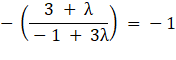
⇒ λ = 2

Substituting the value of λ in (1), we get the equation of the required line.

⇒ 3 + 2x + -1 + 6y – 5 – 2 = 0

⇒ 5x + 5y – 7 = 0

Hence, equation of required line is 5x + 5y – 7 = 0