Prove that the perpendicular drawn from the point (4, 1) on the join of (2, – 1) and (6 5) divides it in the ratio 5:8.

Question

Philoid · Accepted Answer

Given, A perpendicular drawn from the point (4,1) on the join of (2, – 1) and (6,5)

To Prove: The perpendicular divides the line in the ratio 5:8.

Explanation: Let us Assume,The perpendicular drawn from point C(4,1) on a line joining A(2, – 1) and B(6,5) divide in the ratio k:1 at the point R.

Now, The coordinates of R are:

By using Sectional Formula, (x,y) =

R(x,y) = – – – (1)

The slope of the line with two points is, m =

The slope of AB =

The slope of CR =

And, PR is perpendicular to AB

Since, (Slope of CR)×(Slope of AB) = – 1

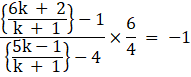
3(4k – 2) = – 2(2k – 2)

12k – 6 = – 4k + 4

16k = 10

K

So, The ratio is 5:8

Hence, R divides AB in the ratio 5:8.