Find the equations to the altitudes of the triangle whose angular points are A (2, – 2), B(1, 1), and C ( – 1, 0).

A triangle is given with three angular points A (2, – 2), B(1, 1), and C ( – 1, 0)

To Find: Find the equation.

Formula Used: The equation of line is (y – y₁) = m(x – x₁)

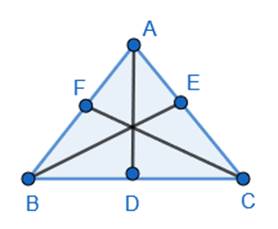
Explanation: Here, AD, BE and CF are the three altitudes of the triangle.

Now,

We know, The slope of the line with two points is, m =

So, The slope of BC =

The slope of AC =

The slope of AB =

and, The product of two slopes of the perpendicular line is always – 1

So, (slope of AB) × (slope of CF) = – 1

The slope of CF =

(slope of BE)×(slope of AC) = – 1

The slope of BE =

(slope of AD)×(slope of BC) = – 1

The slope of AD =

So, The equation of line is (y – y₁) = m(x – x₁)

The equation of Line AD is

y – ( – 2) = – 2(x – 2)

y + 2 = – 2x + 2

2x + y – 2 = 0

The equation of Line BE is

2y – 2 = 3x – 3

2y – 3x + 1 = 0

The equation of Line CF is

x – 3y + 1 = 0

Hence, The equation of the three equation is calculated.