a) What is the principle of transformer?
b) Explain how laminating the core of a transformer helps to reduce eddy current losses in it

c) Why the primary and secondary coils of a transformer are preferably wound on the same core

OR

Show that in the free oscillations of an LC circuit, the sum of energies stored in the capacitor and the inductor is constant in time.

Question

a) What is the principle of transformer?
b) Explain how laminating the core of a transformer helps to reduce eddy current losses in it

c) Why the primary and secondary coils of a transformer are preferably wound on the same core

OR

Show that in the free oscillations of an LC circuit, the sum of energies stored in the capacitor and the inductor is constant in time.

Philoid · Accepted Answer

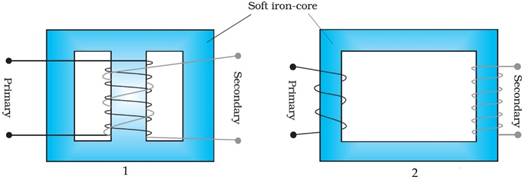
a) Transformer using the principle of mutual induction. A transformer consists of two sets of coils, insulated from each other. They are wound on a soft-iron core, either one on top of the other as shown in the diagram 1 or on separate limbs of the core as shown in the diagram 2. One of the coils called the primary coil has N_P turns. The other coil is called the secondary coil; it has N_P turns.

b) Lamination is done to reduce the eddy current loss by increasing the resistance of the core. The core is made up of thin sheets of steel, therby having relatively high resistance, each lamination being insulated from others by a thin layer of varnish. The planes of these sheets are placed perpendicular to the direction of the current that would be set up by the induced emf. The planes of these sheets are arranged parallel to the magnetic fields so that they can cut across the eddy current paths. Thus, the laminated sheet will have an eddy current that circulates within it but the sum of individual eddy currents of all such laminations are very less compared to that of using single solid iron core.

c) The primary and secondary coils of a transformer are preferably wound on the same core so as to reduce the flux losses and thereby increasing the efficiency of the transformer.

OR

Formula: -

The total energy in the system can be written as,

Where L is value of inductance, C is the value of capacitance, i(t ) and q(t), are the current and charge depending upon the time respectively.
Calculations: -

We can write,

Also, we know that,

i₀=ω₀ q₀

And,

Which gives,

⇒q₀=i₀ √(LC)

Using the above result, we can write,

So, the total energy is,

Which is independent of time and so is a constant.

Conclusions: -

The total energy of the system at any given time is,

which is a constant so the total energy remains constant all the time.