(a) A particle of charge q is moving with velocity v in the presence of crossed Electric field E and Magnetic field B as shown. Write the condition under which the particle will continue moving along x-axis. How would the trajectory of the particle be affected if the electric field is switched off?

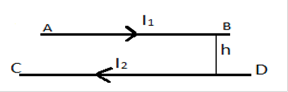
(b) A horizontal wire AB of length ‘l’ and mass ‘m’ carries a steady current I1, free to move in the vertical plane is in equilibrium at the height of ‘h’ over another parallel long wire CD carrying a steady current I2, which is fixed in a horizontal plane as shown. Derive the expression for the force acting per unit length on the wire AB and write the condition for which wire AB is in equilibrium.

OR

(a) An electron in the ground state of a Hydrogen atom is revolving in a circular orbit of radius R. Obtain the expression for the orbital magnetic moment of the electron in terms of fundamental constants.

(b) Draw the magnetic field lines for a current carrying solenoid when a rod made of (i) copper, (ii) aluminium and (iii) iron are inserted within the solenoid as shown.

(a) If the Charged particle has to go undeflected, then there should be no force experienced by it, or resultant of all the forces on the particle is zero. here Charged particle is experiencing Magnetic Lorentz force and the electrostatic force

due to the electric field

We know the Magnetic Lorentz Force is given by

Where F is the force on the Charged particle having charge q, moving with a velocity in a magnetic Field B

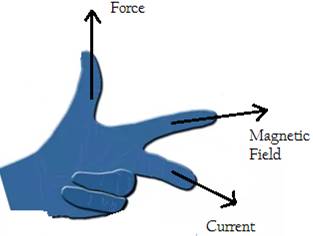
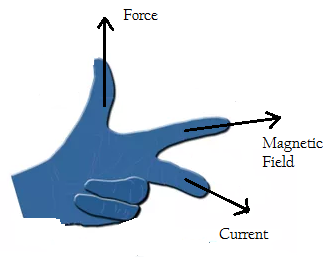
The direction of the Magnetic force is perpendicular to the plane containing V and B. and for a positively charged particle can be found out with the help of Fleming’s left-hand thumb rule.

Flemings rule: If the stretch our forefinger middle finger and thumb mutually perpendicular to each other then if forefinger depicts the direction of magnetic field, middle finger depicts the direction of the current(Direction of Velocity of Positive Charge) then, Thumb depicts the direction of Force.

The electrostatic force is given by

Where F is the force experienced by a particle having charge q and moving in an electric field E, the direction of the force is same as that of Electric field for a positively charged particle and is exactly reversed in case of a negatively charged particle.

So both the forces on particle should be equal in magnitude and opposite in direction.

Since Electric Field is in along Positive Y axis, and the particle has a charge q, so the force on it should be towards Positive Y axis .so force due to the magnetic field should be towards Negative Y direction.As shown in figure

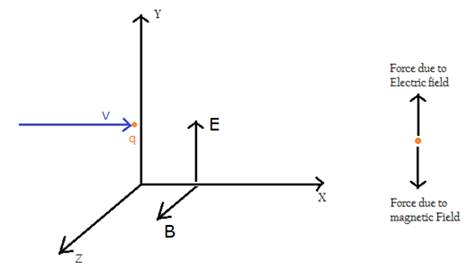
Using the fleming left-hand rule, we will decide the direction of the magnetic field

Applying the rule

Since charged Particle is moving in positive X direction same is the direction of the current, depicted by the middle finger, force should be towards negative Y direction depicted by our thumb, so we find our forefinger depicting magnetic field is in Positive Z direction

Now equating magnitude of both the forces

Here because Velocity of the particle is perpendicular to Magnetic field,

So,

i.e.

or magnitude of the magnetic field Is given by

, directed towards the positive Z axis

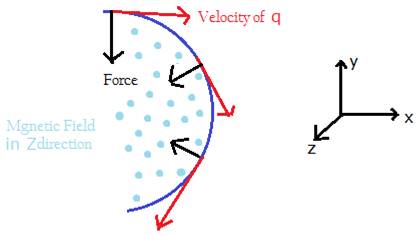
If the electric field is switched off, there will be no force acting on charge q along Positive Y direction, and it will experience a force along the negative Y-axis, and its direction is changed, but again force is perpendicular to velocity since it is still moving perpendicular to field, and at each instant force is perpendicular to its velocity, i.e. causing it to move in helical Trajectory

as shown in figure

(b) We know when a conductor or a long straight wire carries current, magnetic fields are produced around the conductor in closed loops whose magnitude is given by equation

Where B is the magnitude of the magnetic field

I is the current in the wire

R is the distance from the wire at which Magnetic field is being measured

is the permittivity of free space = 4π × 10^-7 TmA^-1

The direction of the induced magnetic field coil can be found with the help of Right Hand Thumb Rule. As Shown in the figure.

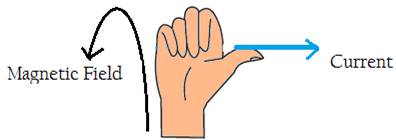
Explanation: if we curl our fingers of right hand in such a way that thump points towards the direction of current in wire than at the direction of induced magnetic field clockwise or anticlockwise in a plane perpendicular to direction of current will be shown by direction of curl fingers, direction at any particular point will be tangent to the circular loop at that point.

Now we also know that a current carrying wire held perpendicular to a magnetic experience force, which is given by equation

F = BIL

Where F is the force experienced by wire of length L, through which current I is flowing and is held in a magnetic field B

The direction of force is given by Fleming’s left-hand rule

Flemings rule: If the stretch our forefinger middle finger and thumb mutually perpendicular to each other then if forefinger depicts the direction of magnetic field, middle finger depicts the direction of the current then, Thumb depicts the direction of Force.

Now in the situation shown

Due to wire CD, there will be magnetic field produced, which will exert a force on wire AB

Now current in wire CD is towards left so curling our fingers with the thumb pointing to left we get that magnitude of the magnitude of magnetic field height h above wire CD where wire AB is placed is vertically inwards to the plane containing wire AB and CD

As shown in the figure

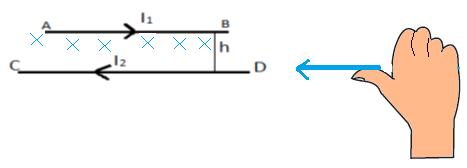
The magnitude of the magnetic field will be given by equation

Where B is the magnitude of the magnetic field

I is the current in the wire

Here, I = I₁

R is the distance from the wire at which Magnetic field is being measured

Here, R = h

is the permittivity of free space = 4π × 10^-7 TmA^-1

i.e. the magnetic field is

Now due to magnetic field force on wire will be given by left hand thumb rule as magnetic field is in vertically inward direction(inward to plane containing AB and CD) denoted by forefinger, current towards right represented by middle finger, so thumb will represent direction of current which in vertically upward direction, now magnitude of force is given as

F = BIL

Where F is the force experienced by wire of length L,

Here L = l

I is the current flowing in the wire

Here I = I₂

B is the magnetic field

Here

So net force experienced by wire AB is

On re-arranging the equation, we get force acting per unit length on wire AB is

The direction of the force is vertically upwards

Now there is a downward force acting on wire due to its weight, which is given as

W = mg

Where W is the weight of wire, m is the mass of wire and is acceleration due to gravity, the free body diagram of wire AB

is as shown below

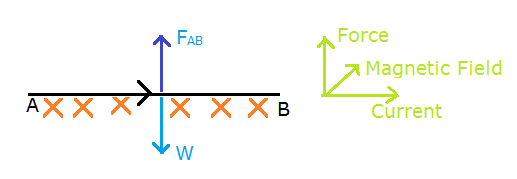
The weight of wire and magnetic force on the wire are acting in the opposite direction but for the wire to be in equilibrium both should be equal in magnitude

i.e. F_AB = W

so equating both we get

This is the required condition for the wire to be in equilibrium.

OR

(a) Let un consider an electron is revolving in a circular orbit of radius R around the nucleus of a hydrogen atom consisting of one proton, the electron is in the ground state, i.e. first orbit or the lowest allowed energy level, if n denotes the energy state in which electron is present then

n = 1

Now due to the motion of electron current is generated, whose direction is opposite to the motion of electron as current is defined as the rate of flow of positive charge and electron is negatively charged

The situation has been shown in figure

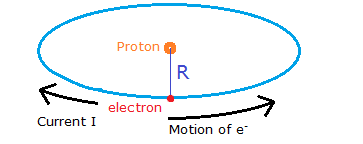
Now we know magnetic moment current flowing in a closed loop is given as