In Fig., PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB || CD.

Question

Philoid · Accepted Answer

Given: Two mirrors are parallel to each other, PQ||RS

To Prove: AB || CD

Proof:

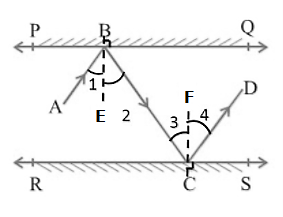
Take two perpendiculars BE and CF, As the mirrors are parallel to each other their perpendiculars will also be parallel thus BE || CF

According to laws of reflection, we know that:

Angle of incidence = Angle of reflection

∠1 = ∠2 and,

∠3 = ∠4 (i)

And,

∠2 = ∠3 (Alternate interior angles, since BE, is parallel to CF and a transversal line BC cuts them at B and C respectively) (ii)

We need to prove that ∠ABC = ∠DCB

∠ABC = ∠1 + ∠2 and ∠DCB = ∠3 + ∠4

From (i) and (ii), we get

∠1 + ∠2 = ∠3 + ∠4

⇒ ∠ABC = ∠DCB

⇒ AB parallel CD (Alternate interior angles)

Hence, Proved.