In Fig. 4.143, ∠A = ∠CED, prove that Δ CAB ∼ Δ CED. Also, find the value of x.

Given: ∠A = ∠CED
To prove: Δ CAB ∼ Δ CED
To find: The value of x.
Theorem Used:
If two triangles are similar, then the ratio of their corresponding sides are equal.
Explanation:
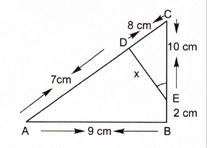
We have, ∠A = ∠CED
In ΔCAB and ΔCED
∠C = ∠C (Common)
∠A = ∠CED (Given)
Then, ΔCAB ~ ΔCED (By AA similarity)
As corresponding parts of similar triangle are proportional.
So,
![]()
Substituting the given values, we get,
![]()
⇒ 15x = 90
⇒ x = 90/15
⇒ x = 6cm
8