Prove that the segment joining the points of contact of two parallel tangents passes through the centre.

Given: Two parallel tangents.

To find: The line through centre is a straight line.

Theorem Used:

Tangent to a circle at a point is perpendicular to the radius through the point of contact.

Explanation:

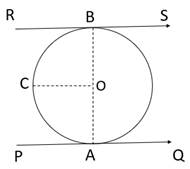
Let PAQ and RBS be two tangents to the circle.

Join OA and OB.

Draw OC||RB

As we know sum of angles on same side of transversal is 180°.

⇒ ∠RBO + ∠COB = 180°

As RB is tangent to the radius OB,

From the theorem stated above,

∠RBO = 90°

⇒ 90° + ∠COB = 180°

⇒ ∠COB = 90°

Similarly, ∠COA = 90°

⇒ ∠COA + ∠COB = 90° + 90°

= 180°

As we know straight line makes an angle of 180° at the centre,

Hence AOB is a straight line passing through O.

Hence proved