In Fig. 10.67, OQ: PQ=3:4 and perimeter of ΔPOQ = 60 cm. Determine PQ, OR and OP.

Given: perimeter of ΔPOQ = 60 cm

To find: the length of PQ, OR and OP

Theorem Used:

1) Tangent to a circle at a point is perpendicular to the radius through the point of contact.

2) Pythagoras theorem:

In a right-angled triangle, the squares of the hypotenuse is equal to the sum of the squares of the other two sides.

Explanation:

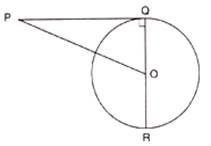
Given that OQ: PQ=3:4

Let ratio coefficient =x, so

OQ = 3x and PQ = 4x

Since QP is tangent to the radius OQ.

By the theorem (1) stated,

∠OQP = 90°

Then applying Pythagoras theorem in triangle POQ

OP²=OQ²+PQ²
OP²=(3x)²+(4x)²
OP²=9x²+16x²
OP²=25x²
OP=5x
Perimeter of a ΔPOQ =60cm,

So,
3x+4x+5x=60
12x=60
x=5
So,
OQ=3x=15cm
PQ=4x=20cm
OP=5x=25cm
QR=2(OQ)=2×15=30cm