In Fig, a circle is inscribed in a quadrilateral ABCD in which ∠B=90°. If AD = 23 cm, AB = 29 cm and DS = 5 cm, find the radius r of the circle.

Given: AD = 23 cm

AB = 29 cm

DS = 5 cm

∠B=90°

To find: The value of r.

Theorem Used:

1) The length of two tangents drawn from an external point are equal.

2.) Tangent to a circle at a point is perpendicular to the radius through the point of contact.

Explanation:

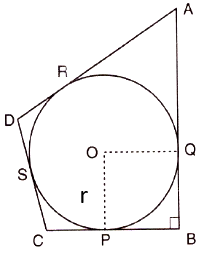
AB, BC, CD and AD are tangents to the circle with centre O at Q, P, S and R respectively.
D is an external point and DR and DS are the tangents drawn from it.

From the theorem (1) stated,
DS = DR = 5 cm
∴ AR = AD – DR = 23 – 5 = 18 cm

A is an external point and AQ and AR are the tangents drawn from it.

From the theorem (1) stated,
AQ = AR = 18 cm
∴ QB = AB – AQ = 29 − 18 = 11 cm

B is an external point and QB and BP are the tangents drawn from it.

From the theorem (1) stated,
QB = BP = 11 cm.
∠PBQ = 90° [Given]

From the theorem (2) stated,
∠OPB = 90°
∠OQB = 90°

As we know sum of angles of a quadrilateral is 360°.

In quadrilateral POQB,

∠POQ + ∠OQB + ∠OPB + ∠QBP = 360°

⇒∠POQ + 90° + 90° + 90° = 360°

⇒∠POQ + 270° = 360°

⇒∠POQ = 90°
So, OQBP is a square.
∴QB = BP = r = 11 cm