CDE is an equilateral triangle formed on a side CD of a square ABCD. Show that Δ ADE ≅ Δ BCE.

Given: An equilateral triangle CDE is on side CD of square ABCD

To prove: ∆ADE ≅ ∆BCE

Proof:

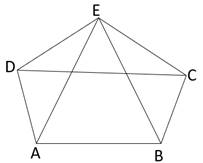
∠EDC = ∠DCE = ∠CED = 60^o (Angles of equilateral triangle)

∠ABC = ∠BCD = ∠CDA = ∠DAB = 90^o (Angles of square)

∠EDA = ∠EDC + ∠CDA

= 60^o + 90^o

= 150^o (i)

Similarly,

∠ECB = 150^o (ii)

In

ED = EC (Sides of equilateral triangle)

AD = BC (Sides of square)

∠EDA = ∠ECB [From (i) and (ii)]

Therefore, By SAS theorem