Show that the function f given by f(x) = tan-1(sinx + cosx), x > 0 is always strictly increasing function in ![]() .
.
f(x) = tan-1(sinx + cosx)
f(x) is strictly increasing in ![]() if f’(x) > 0 when x is between 0 and
if f’(x) > 0 when x is between 0 and ![]()
let us find f’(x)
differentiating f(x)
![]()
![]()
Since sin2x + cos2 = 1 and 2sinxcosx = sin2x
![]()
![]()
![]()
Consider the numerator cosx – sinx
Observe that from graph cosx > sinx when x is in between 0 and ![]()
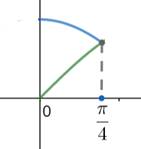
Blue is cosx and green is sinx
Hence cosx – sinx is positive
Now consider the denominator 2 + sin2x
When x is in ![]() sin2x is in
sin2x is in ![]() that is (0, 1)
that is (0, 1)
Hence 2 + sin2x is also positive
As both numerator and denominator are positive hence f’(x) is also positive that is f’(x) > 0
Hence the function f(x) is strictly increasing in ![]()
24