Using integration, find the area of the triangle formed by the positive x-axis and tangent and normal to the circle x² + y² = 4 at (1, √3).

Question

Using integration, find the area of the triangle formed by the positive x-axis and tangent and normal to the circle x 2 + y 2 = 4 at (1, √3).

Philoid · Accepted Answer

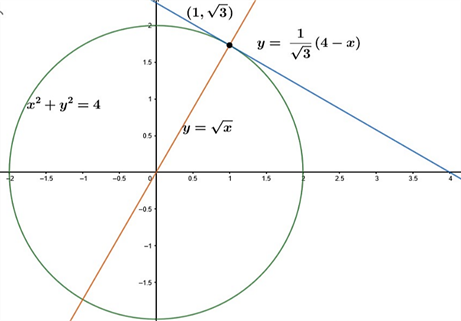
Given; Circle x² + y² = 4 at (1, √3)

Differentiating w.r.t x

∴ The equation of Tangent is;

∴ The equation of Normal is;

Area of the region bounded by the curve y=f(x), the x-axis and the ordinates x=a and x=b, where f(x) is a continuous function defined on [a,b], is given by .

Required Area

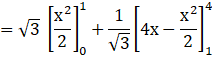
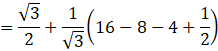
= 2√3 sq.units

Using integration, find the area of the triangle formed by the positive x-axis and tangent and normal to the circle x2 + y2 = 4 at (1, √3).

Using integration, find the area of the triangle formed by the positive x-axis and tangent and normal to the circle x² + y² = 4 at (1, √3).