Find non-zero values of x satisfying the matrix equation:

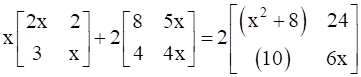
A matrix, as we know, is a rectangular array of numbers, symbols, or expressions, arranged in rows and columns.

Also,

Two or more matrices can be added or subtracted only if they have same order.

And we are familiar with order of a matrix. If a matrix has M rows and N columns, the order of matrix is M × N.

We have matrix equation,

Take matrix .

Multiply it with x,

…(i)

Take matrix .

Multiply it with 2,

…(ii)

Take matrix .

Multiply it with 2,

…(iii)

Add equation (i) and (ii) and make it equal to equation (iii), we get

Adding left side of the matrix equation as they have same order.

We need to find the value of x.

So, compare the elements in the two matrices.

If,

Then,

a₁₁ = b₁₁

a₁₂ = b₁₂

a₂₁ = b₂₁

a₂₂ = b₂₂

So,

2x² + 16 = 2(x² + 8) …(i)

2x + 10x = 48 …(ii)

3x + 8 = 20 …(iii)

x² + 8x = 12x …(iv)

We have got equations (i), (ii), (iii) and (iv) to solve for x.

So, take equation (i).

2x² + 16 = 2x² + 16

We won’t be able to find x from this equation, as both equations are same.

Now, take equation (ii).

2x + 10x = 48

⇒ 12x = 48

⇒ x = 4

From equation (iii),

3x + 8 = 20

⇒ 3x = 20 – 8

⇒ 3x = 12

⇒ x = 4

From equation (iv),

x² + 8x = 12x

⇒ x² = 12x – 8x

⇒ x² = 4x

⇒ x² – 4x = 0

⇒ x(x – 4) = 0

⇒ x = 0 or (x – 4) = 0

⇒ x = 0 or x = 4

⇒ x = 4 (∵ x = 0 does not satisfy equations (ii) and (iii))

So, by solving equations (ii), (iii) and (iv), we can conclude that

x = 4

Thus, the value of x is 4.