Show that 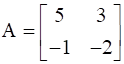satisfies the equation A² – 3A – 7I = 0 and hence find A^–1.

We have the matrix A, such that

(i). We need to show that the matrix A satisfies the equation A² – 3A – 7I = 0.

(ii). Also, we need to find A^-1.

(i). Take L.H.S: A² – 3A – 7I

First, compute A².

A² = A.A

In order to multiply two matrices, A and B, the number of columns in A must equal the number of rows in B. Thus, if A is an m x n matrix and B is an r x s matrix, n = r.

Multiply 1^st row of matrix A by matching members of 1^st column of matrix A, then sum them up.

(5, 3).(5, -1) = (5 × 5) + (3 × -1)

⇒ (5, 3).(5, -1) = 25 + (-3)

⇒ (5, 3).(5, -1) = 25 – 3

⇒ (5, 3).(5, -1) = 22

Multiply 1^st row of matrix A by matching members of 2^nd column of matrix A, then sum them up.

(5, 3).(3, -2) = (5 × 3) + (3 × -2)

⇒ (5, 3).(3, -2) = 15 + (-6)

⇒ (5, 3).(3, -2) = 15 – 6

⇒ (5, 3).(3, -2) = 9

Multiply 2^nd row of matrix A by matching members of 1^st column of matrix A, then sum them up.

(-1, -2).(5, -1) = (-1 × 5) + (-2 × -1)

⇒ (-1, -2).(5, -1) = -5 + 2

⇒ (-1, -2).(5, -1) = -3

Multiply 2^nd row of matrix A by matching members of 2^nd column of matrix A, then sum them up.

(-1, -2).(3, -2) = (-1 × 3) + (-2 × -2)

⇒ (-1, -2).(3, -2) = -3 + 4

⇒ (-1, -2).(3, -2) = 1

Substitute values of A² and A in A² – 3A – 7I.

Also, since matrix A is of the order 2 × 2, then I will be the identity matrix of order 2 × 2 such that,

Clearly,

L.H.S = R.H.S

Thus, we have shown that matrix A satisfy A² – 3A – 7I = 0.

(ii). Now, let us find A^-1.

We know that, inverse of matrix A is A^-1 is true only when

A × A^-1 = A^-1 × A = I

Where, I = Identity matrix

We have,

A² – 3A – 7I = 0

Multiply A^-1 on both sides, we get

A^-1(A² – 3A – 7I) = A^-1 × 0

⇒ A^-1.A² – A^-1.3A – A^-1.7I = 0

⇒ A^-1.A.A – 3A^-1.A – 7A^-1.I = 0

⇒ (A^-1A)A – 3(A^-1A) – 7(A^-1I) = 0

And as A^-1A = I and A^-1I = A^-1

⇒ IA – 3I – 7A^-1 = 0

Since, IA = A

⇒ A – 3I – 7A^-1 = 0

⇒ 7A^-1 = A – 3I

[∵ ]

Thus, .