Find A, if 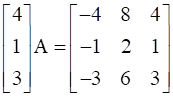 .
.
We have,

We need to find the matrix A.
Let us see what the order of the matrices given are.
We know what order of matrix is,
If a matrix has M rows and N columns, the order of matrix is M × N.
Order of  .
.
Number of rows = 3
⇒ M = 3
Number of column = 1
⇒ N = 1
Then, order of matrix X = M × N
⇒ Order of matrix X = 3 × 1
Order of  .
.
Number of rows = 3
⇒ M = 3
Number of columns = 3
⇒ N = 3
Then, order of matrix Y = M × N
⇒ Order of matrix Y = 3 × 3
We must understand that, when a matrix of order 1 × 3 is multiplied to the matrix X, only then matrix Y is produced.
Let matrix A be of order 1 × 3, and can be represented as
![]()
Then, we get

Take L.H.S: 
In order to multiply two matrices, A and B, the number of columns in A must equal the number of rows in B. Thus, if A is an m x n matrix and B is an r x s matrix, n = r.
So, we have

Multiply 1st row of matrix X by matching member of 1st column of matrix A, then sum them up.
(4)(a) = 4a

Multiply 1st row of matrix X by matching member of 2nd column of matrix A, then sum them up.
(4)(b) = 4b

Multiply 1st row of matrix X by matching member of 3rd column of matrix A, then sum them up.
(4)(c) = 4c

Multiply 2nd row of matrix X by matching member of 1st column of matrix A, then sum them up.
(1)(a) = a

Multiply 2nd row of matrix X by matching member of 2nd column of matrix A, then sum them up.
(1)(b) = b

Multiply 2nd row of matrix X by matching member of 3rd column of matrix A, then sum them up.
(1)(c) = c

Multiply 3rd row of matrix X by matching member of 1st column of matrix A, then sum them up.
(3)(a) = 3a

Multiply 3rd row of matrix X by matching member of 2nd column of matrix A, then sum them up.
(3)(b) = 3b

Multiply 3rd row of matrix X by matching member of 3rd column of matrix A, then sum them up.
(3)(c) = 3c

Now, L.H.S = R.H.S


Since, the matrices on either sides are of same order, we can say that
4a = -4 …(i)
4b = 8 …(ii)
4c = 4 …(iii)
a = -1 …(iv)
b = 2 …(v)
c = 1 …(vi)
3a = -3 …(vii)
3b = 6 …(viii)
3c = 3 …(ix)
From equation (i), we can find the value of a,
4a = -4
![]()
⇒ a = -1
From equation (ii), we can find the value of b,
4b = 8
![]()
⇒ b = 2
From equation (iii), we can find the value of c,
4c = 4
![]()
⇒ c = 1
And it will satisfy other equations (iv), (v), (vi), (vii), (viii) and (ix) too.
Thus, the matrix A is
![]()