Given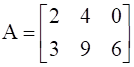 
and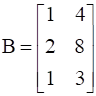 
. Is (AB)’ = B’A’?
We have two matrices A and B, such that
We need to verify whether (AB)’ = B’A’.
Let us understand what a transpose is.
In linear algebra, the transpose of a matrix is an operator which flips a matrix over its diagonal, that is it switches the row and column indices of the matrix by producing another matrix denoted as AT.
Take L.H.S = (AB)’
So, let us compute AB.
Multiply 1st row of matrix A by matching members of 1st column of matrix B, then sum them up.
(2, 4, 0)(1, 2, 1) = (2 × 1) + (4 × 2) + (0 × 1)
⇒ (2, 4, 0)(1, 2, 1) = 2 + 8 + 0
⇒ (2, 4, 0)(1, 2, 1) = 10
Multiply 1st row of matrix A by matching members of 2nd column of matrix B, then sum them up.
(2, 4, 0)(4, 8, 3) = (2 × 4) + (4 × 8) + (0 × 3)
⇒ (2, 4, 0)(4, 8, 3) = 8 + 32 + 0
⇒ (2, 4, 0)(4, 8, 3) = 40
Similarly, let us do it for the rest of the elements.
So,
Now, for transpose of AB, rows will become columns.
Now, take R.H.S = B’A’
If 
Then, if (1, 4) are the elements of 1st row, it will become elements of 1st column, and so on.
Also,
Then, if (2, 4, 0) are the elements of 1st row, it will become elements of 1st column, and so on.
Now, multiply B’A’.
Multiply 1st row of matrix B’ by matching members of 1st column of matrix A’, then sum them up.
(1, 2, 1)(2, 4, 0) = (1 × 2) + (2 × 4) + (1 × 0)
⇒ (1, 2, 1)(2, 4, 0) = 2 + 8 + 0
⇒ (1, 2, 1)(2, 4, 0) = 10
Multiply 1st row of matrix B’ by matching members of 2nd column of matrix A’, then sum them up.
(1, 2, 1)(3, 9, 6) = (1 × 3) + (2 × 9) + (1 × 6)
⇒ (1, 2, 1)(3, 9, 6) = 3 + 18 + 6
⇒ (1, 2, 1)(3, 9, 6) = 27
Similarly, filling up for the rest of the elements.
⇒ L.H.S = R.H.S
Thus, (AB)’ = B’A’.