If 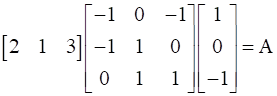, find A.

We are given with a matrix equation,

We need to find A.

Take L.H.S:

Let us solve , where

Then,

Order of X = 1 × 3

Order of Y = 3 × 3

Then, resulting order of matrix Z(say) = 1 × 3 [Let Z = XY]

Multiply 1^st row of matrix X by matching members of 1^st column of matrix Y, then sum them up.

(2, 1, 3)(-1, -1, 0) = (2 × -1) + (1 × -1) + (3 × 0)

⇒ (2, 1, 3)(-1, -1, 0) = -2 – 1 + 0

⇒ (2, 1, 3)(-1, -1, 0) = -3

Multiply 1^st row of matrix X by matching members of 2^nd column of matrix Y, then sum them up.

(2, 1, 3)(0, 1, 1) = (2 × 0) + (1 × 1) + (3 × 1)

⇒ (2, 1, 3)(0, 1, 1) = 0 + 1 + 3

⇒ (2, 1, 3)(0, 1, 1) = 4

Multiply 1^st row of matrix X by matching members of 3^rd column of matric Y, then sum them up.

(2, 1, 3)(-1, 0, 1) = (2 × -1) + (1 × 0) + (3 × 1)

⇒ (2, 1, 3)(-1, 0, 1) = -2 + 0 + 3

⇒ (2, 1, 3)(-1, 0, 1) = 1

So,

Now, multiplying Z by .

Order of Z = 1 × 3

Order of Q = 3 × 1

Then, order of the resulting matrix = 1 × 1

Multiply 1^st row of matrix Z by matching members of 1^st column of matrix Q, then sum them up.

(-3, 4, 1)(1, 0, -1) = (-3 × 1) + (4 × 0) + (1 × -1)

⇒ (-3, 4, 1)(1, 0, -1) = -3 + 0 – 1

⇒ (-3, 4, 1)(1, 0, -1) = -4

Now, since

Thus,

A = [-4]