Find inverse, by elementary row operations (if possible), of the following matrices.

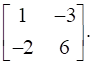
Let B =

To apply elementary row transformations we write:

B = IB where I is the identity matrix

We proceed with operations in such a way that LHS becomes I and the transformations in I give us a new matrix such that

I = XB

And this X is called inverse of B = B^-1

So we have:

Applying R₂→ R₂ + 2R₁

⇒

As we got all zeroes in one of the row of matrix in LHS.

So by any means we can make identity matrix in LHS.

∴ inverse of B does not exist.

B^-1 does not exist. …ans